4. 인터프리터 구현 - 표현식 파싱(1)

게시 2024/06/15

By Gyu Hwan 15 분읽는 시간

1. 파싱을 시작하기 앞서

지금까지 과정으로 스캐너로 토큰도 분류했고 문법도 정리했다. 이제부터 파싱의 시간이 왔다. 개인적으로 이해와 습득을 위해 많은 시간을 들였던 구간이다. 이전 장의 컨택스트 자유 문법과 록스의 문법, 비지터 패턴을 배웠는데. 그래서 ‘이걸로 뭘 하라는거야?’ 라는 생각이 든다. 이번 글은 이것들의 사용 방법과 쓰임새를 이해하기 쉽게 설명해보려고 한다.

스캐너를 통한 토큰 분류

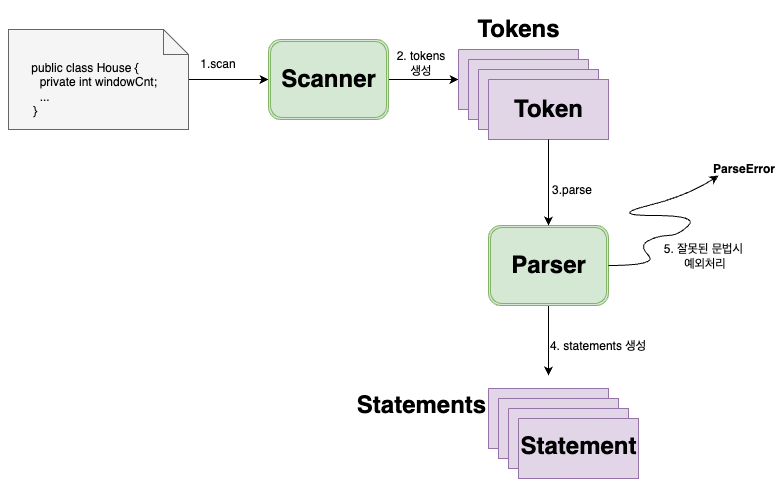
원시 코드를 스캐너를 통해 스캔하고 토큰 뭉치(List)로 반환한다.

파싱이란?

파싱은 토큰들을 문법에 맞추는 과정이다. 잘못된 문법 검증과 문법에 대한 처리까지 일이다. 토큰들을 입력값으로 받아 문법을 확인하고 문장 뭉치(List)로 반환한다. 만약 잘못된 문법이라면 PaseError를 던진다.

이 paser 과정에서 코드 표현에서 만들었던 문법이 사용된다. 미리 만들었던 문법을 다시 살펴보자.

록스 코드 문법

expression -> literal | unary | binary | grouping; literal -> NUMBER | String | “true” | “false” | “nil”; grouping -> “(“ expression “)”; unary -> (“-“|”!”) expression; binary -> expression operator expresision; operator -> “==” | “!=” | “>” | “>=” | “<” | “<=” | “+” | “-“| “*” | “/”;

파싱 클래스에는 이 문법이 재귀 형식으로 그대로 들어가게 된다. 자세한 코드로 들어가기 앞서, 다음의 토큰 예시를 살펴보자.

6 / 3 - 1

이 토큰의 문자열은 컨택스트 자유 문법과 록스 문법을 기준으로 어떤 식으로 파싱될까? 두 가지 방법이 있다.

1) 첫 번째 방법

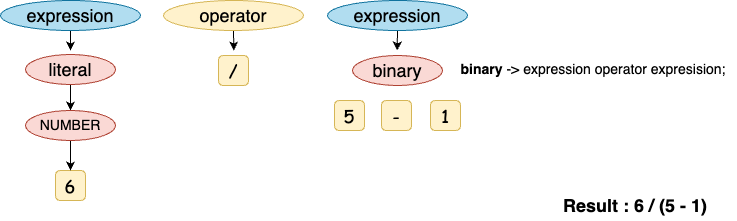
(1) 파싱의 제일 처음은 expression 부터다. 토큰 뭉치에서 제일 앞에 있는 6을 가져온다.

(2) expression에서 갈 수 있는 곳은 literal | unary | binary | grouping이다. 다음 토큰을 확인해보니 토큰의 값이 ‘/’이라는 것을 확인할 수 있다. ‘/’라면 binary가 맞을 것같다. (binary → expression operator expression)

(3) binary로 매칭하고 좌측 expression을 literal → NUMBER 로 고르고 6을 사용한다. (6 operator expression)

(4) operator를 ‘/’ 으로 고른다. (6 / expression)

(5) 우측 expression을 5로 가져오는데. 다음 토큰을 확인하니 ‘-’가 나온다. 다시 binary로 다시 고른다. (6 / binary) ⇒ (6 / expression operator expression)

(6) 동일한 방법으로 binary에 값들을 넣어준다. (6 / (5 - 1))

2) 두 번째 방법

(1) expression 부터 시작한다.

(2) expression에서 갈 수 있는 곳은 ‘literal

unary

binary

grouping’ 이다. 다음 토큰을 확인해보니 ‘/’ 이다. **다음에 갈 곳은 **binary 가 맞을 것 같다. (binary → expression operator expression)

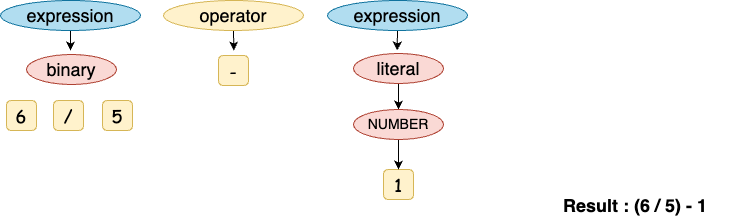
(3) 여기부터 첫 번째 방법과 다르다. 처음 expression을 literal이 아닌 binary로 고른다. 그리고 각각 6 / 5를 선택한다.

(4) 바깥쪽으로 나와 operator를 ‘-’로 고른다.

(5) 우측 expression을 NUMBER로 고르고 1을 사용한다. ((6 / 5) - 1)

동일한 문법을 사용했는데. 나올 수 있는 가지 수가 두 가지다. 6 / (5 - 1)이거나 (6 / 5) - 1 인데. 일반적인 상식으론 후자가 맞을거다. 이유는 ‘/’, ‘*’가 나머지 연산자보다 우선순위가 더 높기 때문이다. 만약 연산자의 우선순위가 모두 동일하다면 어떨까? 6 + 2 - 1 + 5 의 연산자의 우선순위는 모두 동일하다. 이럴땐 일반적으로 좌측부터 계산한다. 이를 좌측 결합이라고 하는데. 좌측 결합이란 좌측에 있는 연산자를 우측에 있는 연산자보다 먼저 평가하는 것을 의미한다.

이처럼 올바른 계산을 위해선 우선순위와 결합 법칙을 먼저 정의하는게 중요하다.

우선순위와 결합법칙

다음은 우선 순위가 가장 낮은 것부터 높은 것 순서대로 정리한 테이블이다.

명칭	연산자	결합 법칙
동등(equality)	== !=	좌측
비교(comparison)	> ≥ < ≤	좌측
항(term)	- +	좌측
인수(factor)	/ *	좌측
단항(unary)	! -	우측

록스 표현식 업데이트

다음은 우선 순위와 규칙에 맞게 록스 표현식을 업데이트한 버전이다.

문법 표기	코드표현
터미널	토큰을 매치하여 소비하는 코드
넌터미널	해당 규칙의 함수를 호출
\|	if 또는 switch문
* 또는 +	while 또는 for문
?	if 문

expression → equality;

equality → comparison ( (”≠” | “==”) comparison)*;

comparison → term( ( ”>” | “≥” | “<” | “≤” ) term)*;

term → factor( ( ”-” | ”+” ) factor)*;

factor → unary( ( ”/” | “” ) unary);

unary → ( ”!” | “-” ) unary | primary;

2. 파싱 구현

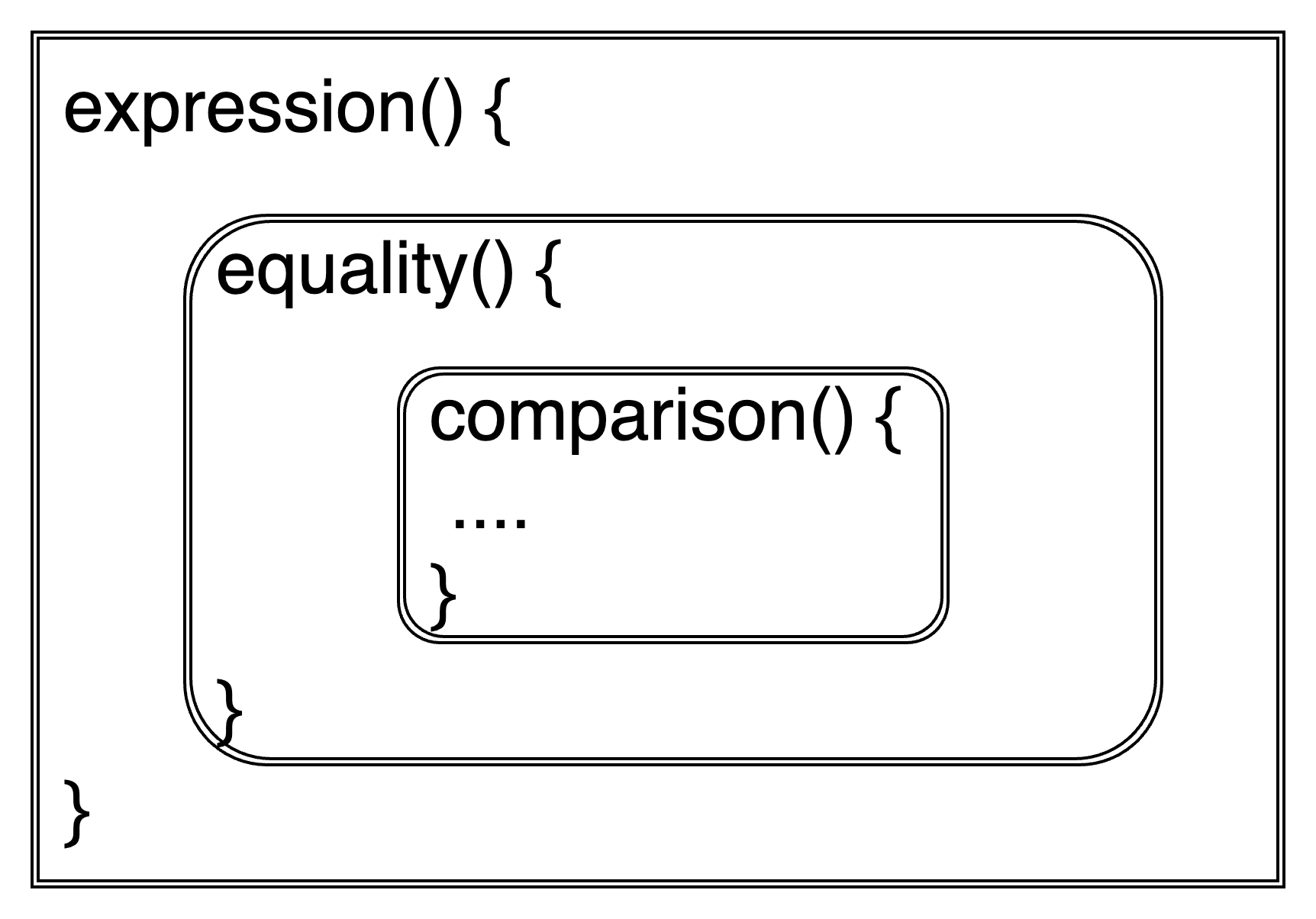
재귀 하향 파싱

재귀 하향이란 이름에서 알 수 있듯, 위에서부터 재귀적으로 아래로 이동하는 것을 의미한다. 이러한 재귀적인 모습을 이미지로 표현한다면 아래와 같다.

파서 클래스

스캐너가 플랫한 입력된 시퀀스를 소비하지만, 파서는 문자 대신 토큰을 소비한다.

  
class Parser{
	private final List<Token> tokens;
	private int current = 0;
	
	Parser(List<Token> tokens){
		this.tokens = tokens;
	}
}

current는 현재 파싱할 토큰의 위치를 가리킨다. 이제 위에 있던 록스 표현식을 코드로 옮겨보자.

1) expression → equality

  
private Expr expression(){
	return equality();
}

2) equality → comparison ( (”≠” | “==”) comparison)*;

  
private Expr equality() {
	Expr expr = comparison();
	
	while(match(EQUAL_EQUAL, BANG_EQUAL)){
		Token operator = previous();
		Expr right = comparison();
		expr = new Expr.Binary(expr, operator, right);
	}
	return expr;
}

equality 하나를 살펴보면 나머지 문법은 거의 동일하다. 이해하기 쉽게 예시와 함께 살펴보자.

‘1 == 2’ 라는 코드가 있을 때, 처음 Expr expr = comparison()를 거치면서(자세한 구현은 아래에 나올 것이다.) 숫자 1을 담을 것이다. match 메소드는 두 가지 일을 한다. 하나는 현재 토큰이 인자와 일치하는지와 일치하면 current의 값을 증가시킨다. 가능하면 한 가지 일을 하는게 이해하기 쉬운데. 저자는 이 방식을 택했다.
while 문을 통해 ‘==’ or ‘!=’ 가 있다면 true를 반환함과 동시에 current 의 값을 증가시킨다.
previous 메서드는 current - 1 의 토큰을 가져온다. 예시로는 == 값이 담긴 토큰을 가져온다.
right는 처음 1을 담을 때와 동일하게 숫자 2를 오른쪽 값을 담게 된다.

결과는 Expr.Binary 에 담는다.

match

  
  // 토큰 확인과 현재 위치 증가
  private boolean match(TokenType... types) {
  	for(Tokentype type: types) {
  		if(check(type)){
  			advance();
  			return true;
  		}
  	} 
  	return false;
  }

check

  
  // 현재 위치의 타입 확인
  private boolean check(TokenType type) {
  	if(isAtEnd()) return false;
  	return peek().type == type;
  }

advance()

  
  // 현재 위치 증가와 현재 토큰 반환
  private Token advance() {
  	if(!isAtEnd()) current++;
  	return previous();
  }

peek, isAtEnd, previous

  
  // 토큰의 마지막인지 확인
  private boolean isAtEnd() {
  	return peek().type = EOF;
  }
    
  // 현재 위치의 토큰 값 반환
  private Token peek() {
  	return tokens.get(current);
  }
    
  // 이전 위치의 토큰 값 반환
  private Token previous() {
  	return tokens.get(current - 1);
  }

3) comparison → term( ( ”>” | “≥” | “<”| “≤” ) term)*;

  
private Expr comparison() {
	Expr expr = term();
	
	while(match(GREATER, GREATER_EQUAL, LESS, LESS_EQUAL)) {
		Token operator = previous();
		Expr right = term();
		return new Expr.Binary(expr, operator, right);
	}
	return expr;
}

comparison은 실상 equality와 토큰 타입만 다르지 코드는 동일하다.

4) term → factor( ( ”-” | ”+” ) factor)*;

  
private Expr term() {
	Expr expr = factor();
	
	while(match(MINUS, PLUS)){
		Token operator = previous();
		Expr right = factor();
		return new Expr.Binary(expr, operator, right);
	}
	return expr;
}

5) factor → unary( ( ”/” | “” ) unary);

  
private Expr factor(){
	Expr expr = unary();
	
	while(match(SLASH, STAR)){
		Token operator = previous();
		Expr right = unary();
		return new Expr.Binary(expr, operator, right);
	}
	return expr;;
}

6) unary → ( ”!” | “-” ) unary | primary;

  
private Expr unary() {
	if(match(BANG, MINUS)){
		Token operator = previous();
		Expr right = unary();
		return Expr.Unary(operator, right);
	}
	return primary();
}

단항식부터는 조금 다르다. 먼저 ‘!’, ‘-’ 와 같은지 확인하고 같다면 Unary에 담아서 반환다. 여기서 Expr right = unary()가 왜 나오는지 의문일 수 있다.

Expr right = primary()가 아닌가 할 수 있는데. 록스 문법은 !!true 와 같은 표현식을 허용한다.

아직 말은 안했지만 각각 파싱되는 결과에 따라 Binary, Unary 객체에 담고있는데. 이에 대한 처리는 비지터 패턴와 함께 다음 내용으로 작성하겠다.

7) primary → NUMBER | String | “true” | “false” | “nil” | “(” expression “)”;

  
private Expr primary() {
	if(match(FALSE)) return Expr.Literal(false);
	if(match(TRUE)) return Expr.Literal(true);
	if(match(NIL)) return Expr.Literal(null);
	
	if(match(NUMBER, String)) return Expr.Literal(previous().literal);
	
	if(match(LEFT_PAREN)) {
		Expr expr = expression();
		consume(RIGHT_PAREN, "Expect ')' after expression");
		return new Expr.Grouping(expr);
	}
}

primary는 간단하다. false, true, nil, NUMBER, String을 구분해서 Literal 객체에 담아준다. LEFT_PAREN은 ‘(’을 의미한다. 가운데 표현식을 파싱하고 ‘RIGHT_PAREN’ 이 없으면 예외를 던진다.

3. 리팩터링

코드를 보다보면 중복된 부분이 보인다. equality, comparison, term, factor 메서드 모두 아래와 같은 구조를 갖는걸 확인할 수 있다.

  
private Expr 메서드명() {
	Expr expr = 상위문법();
	
	while(match(현재 확인할 토큰들)){
		Token operator = previous();
		Expr right = 상위문법()
		expr = new Expr.Binary(expr, operator, right);
	}
	return expr;
}

자바 8의 함수형 인터페이스를 사용하여 핸들러 메서드를 만들어보자

  
private Expr parseLeftAssociativeBinaryExpr(Supplier<Expr> operandParser,
 TokenType... operatorTypes){
	Expr expr = operandParser.get();
	
	while(match(operatorTypes)){
		Toekn operator = previous();
		Expr right = operandParser.get();
		expr = new Expr.Binary(expr, operator, right);
	}
	return expr;
}

private Expr equality() {
 return parseLeftAssociativeBinaryExpr(this::comparison, BANG_EQUAL, EQUAL_EQUAL);
}

private Expr comparison() {
  return parseLeftAssociativeBinaryExpr(this::term, GREATER, GREATER_EQUAL, LESS, LESS_EQUAL);
}

private Expr term() {
  return parseLeftAssociativeBinaryExpr(this::factor, MINUS, PLUS);
}

private Expr factor() {
  return parseLeftAssociativeBinaryExpr(this::unary, SLASH, STAR);
}

Interpreter, Java

Interpreter